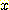 , 분류하고자 하는 class를
, 분류하고자 하는 class를 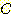 , 전체 모집단에서 변수
, 전체 모집단에서 변수 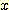 에 대한 확률분포를
에 대한 확률분포를 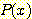 , 임의의 sample 이 class
, 임의의 sample 이 class 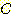 에 속할 사전확률
에 속할 사전확률 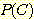 , class
, class 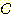 에서 변수 값
에서 변수 값 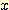 가 얻어질 조건부 확률
가 얻어질 조건부 확률 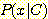 이 주어진다.
이 주어진다.
Pattern Recognition and Image Analysis : Earl Gose. Richard Johnsonbaugh. Steve Jost 저서, Prentice Hall, 1996, Page 81~115
3.4 Conditional Independent Features
Two-Dimensional Decision Boundaries
d-dimensional Decision Boundaries in Matrix Notation
3.6 Unequal Costs of Error
3.7 Estimation of Error Rates
3.8 The Leaving-One-Out Technique
3.9 Characteristic Curves
3.10 Estimating the Composition of Populations
이것은 확률이론에 근거한 decision making 또는 classification을 의미한다.즉 data로부터 추출된 parameter들을 포함한다. Statistical Decision Making 라고도 한다.
자동 패턴인식에서는 supervised learning 이라는 말을 사용한다. 즉 구분하려고 하는 각 class에 대한 density function을 잘 알고 있다는 가정에서 시작한다. 관련된 sample data에서 parameter들을 추출하고 density를 알아내어 패턴인식 과정을 수행한다.
즉 알려져있는 class의 패턴들의 training set을 사용해서 특정 decision making 기술로서 미래의 유사한 sample들을 classify해내는 pattern classifier를 설계하는 과정을 의미한다. 달리 말하면 training data를 사용해서 설계되는 classifier이다. 각 패턴에 대한 class가 알려져있는 분리된 test set을 사용해서 새로운 data에 대해 classifier가 편견없는 정확한 분류를 할 수 있게 해준다.
Bayes' 정리를 이용한 의사 결정은 feature 값이 주어진 상태에서 가장 가능성이 있는 class를 선택하는 것을 말한다. 즉 Bayes' 정리를 이용하여 class membership 의 확률이 계산된다. 여기서는 하나의 변수 (single feature) 의 값에 기초한 classification을 언급한다.
변수 값을 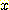 , 분류하고자 하는 class를
, 분류하고자 하는 class를 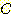 , 전체 모집단에서 변수
, 전체 모집단에서 변수 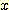 에 대한 확률분포를
에 대한 확률분포를 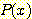 , 임의의 sample 이 class
, 임의의 sample 이 class 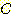 에 속할 사전확률
에 속할 사전확률 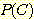 , class
, class 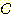 에서 변수 값
에서 변수 값 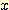 가 얻어질 조건부 확률
가 얻어질 조건부 확률 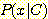 이 주어진다.
이 주어진다.
우리가 얻고자 하는 것은 변수 값 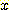 가 주어진 상황에서 sample 이 class
가 주어진 상황에서 sample 이 class 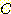 에 속할 확률 즉
에 속할 확률 즉  을 구하는 것인데, 이를 위해
을 구하는 것인데, 이를 위해 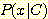 ,
, 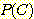 ,
, 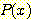 값이 주어진다.
값이 주어진다.
class 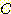 에 속하면서 하나의 변수값
에 속하면서 하나의 변수값 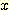 (single feature)를 가지는 경우의 확률은 다음과 같다.
(single feature)를 가지는 경우의 확률은 다음과 같다.
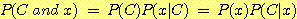
위의 식을 다시 정리하면 다음과 같은 Bayes' 정리가 된다.
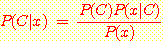
Example 3.1 어떤 사람이 열이 있을 때 감기 일 확률은 얼마인가?
두 개의 class 즉 감기인 경우  와 아닌 경우
와 아닌 경우  로 나눌 수 있다. 열이라고 하는 feature를
로 나눌 수 있다. 열이라고 하는 feature를 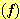 로 두면 그것은 두 개의 값 (열이 있는 것, 열이 없는 것)을 가진다. 어떤 사람이
감기일 사전 확률
로 두면 그것은 두 개의 값 (열이 있는 것, 열이 없는 것)을 가진다. 어떤 사람이
감기일 사전 확률 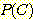 = 0.01 이고, 감기 걸린 사람이 열이 있을 확률
= 0.01 이고, 감기 걸린 사람이 열이 있을 확률 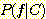 = 0.4 이고, 어떤 사람이 열이 있을 확률 (감기 걸린 사람과 안걸린 사람을 포함해서)
= 0.4 이고, 어떤 사람이 열이 있을 확률 (감기 걸린 사람과 안걸린 사람을 포함해서)
 = 0.02 라고 가정한다. 이럴 경우 열이 있는 사람이 감기에 걸렸을 확률은
다음과 같이 추정된다.
= 0.02 라고 가정한다. 이럴 경우 열이 있는 사람이 감기에 걸렸을 확률은
다음과 같이 추정된다.
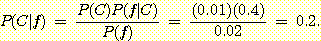
두 개의 class 만 있고 두 개의 값만을 가지는 하나의 feature가 있을 경우를 Venn diagram 으로 그린 그림이다. 이것은 대개 복잡한 문제의 경우에는 해당되지 않는 것이다.
Bayes' 정리를
k 개의 class 의 경우에 적용해보자. class 들이 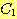 ,.....,
,.....,  가 있고 mutually exclusive 하며 모든 sample 이 class 중의 하나에 반드시
속한다고 가정한다. 만일 최초의 class 정의에서 새로운 sample 이 어떤 class 에도
속하지 않을 가능성이 있다면 새로운 class를 만들어서 그 sample을 포함하게 한다.
최초의 class 정의가 mutually exclusive 하지 않을 경우 새로운 mutually exclusive
class들을 정의하여 최초의 class 멤버의 가능한 조합을 취하도록 정의될 수 있다.
예를들면 하나의 sample이 class
가 있고 mutually exclusive 하며 모든 sample 이 class 중의 하나에 반드시
속한다고 가정한다. 만일 최초의 class 정의에서 새로운 sample 이 어떤 class 에도
속하지 않을 가능성이 있다면 새로운 class를 만들어서 그 sample을 포함하게 한다.
최초의 class 정의가 mutually exclusive 하지 않을 경우 새로운 mutually exclusive
class들을 정의하여 최초의 class 멤버의 가능한 조합을 취하도록 정의될 수 있다.
예를들면 하나의 sample이 class 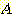 또는
또는 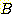 에 속하거나 둘다에 속하거나 둘다에 속하지 않을 수가 있을 경우 다음과 같은
4 개의 새로운 mutually exclusive class (
에 속하거나 둘다에 속하거나 둘다에 속하지 않을 수가 있을 경우 다음과 같은
4 개의 새로운 mutually exclusive class ( 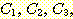
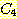 ) 들이 정의 될 수 있다.
) 들이 정의 될 수 있다.
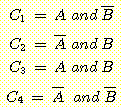
대개 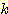 개의 class 에 대해
개의 class 에 대해 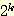 개의 mutually exclusive class 들이 정의 될 수 있다. 만일 가능한 조합의 수가
너무 크면 이용할 수 있는 data 의 양이 작게 될 것이고 따라서 확률의 정확한 근사치를
주지 않을 것이다.
개의 mutually exclusive class 들이 정의 될 수 있다. 만일 가능한 조합의 수가
너무 크면 이용할 수 있는 data 의 양이 작게 될 것이고 따라서 확률의 정확한 근사치를
주지 않을 것이다.
하나의 sample이 하나 이상의 class 에 속할 수
있는 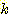 -class 문제를 해결하는 다른 방법은
-class 문제를 해결하는 다른 방법은 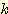 개의 분리된 two class 문제로서 나누는 것이다. 즉 그 sample 이 class
개의 분리된 two class 문제로서 나누는 것이다. 즉 그 sample 이 class 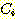 에 속하느냐 아니냐? 고 묻는 것이다. 이러한 방법의 단점은 "not
에 속하느냐 아니냐? 고 묻는 것이다. 이러한 방법의 단점은 "not 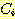 " 인 class를 묘사하기가 어렵다는 것이다. 왜냐하면 그것이 "non
" 인 class를 묘사하기가 어렵다는 것이다. 왜냐하면 그것이 "non 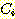 " 인 몇 개의 subclass를 합친 것일 수 있기 때문이다.
" 인 몇 개의 subclass를 합친 것일 수 있기 때문이다.
만일 class  가 mutually exclusive 하며 joint event 인
가 mutually exclusive 하며 joint event 인  가 또한 mutually exclusive 하다면 덧셈 법칙을 사용하여 다음을 구할 수 있다.
가 또한 mutually exclusive 하다면 덧셈 법칙을 사용하여 다음을 구할 수 있다.
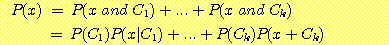 (A)
(A)
class  인 경우의 Bayes' 정리는
인 경우의 Bayes' 정리는

위의 두 식에서 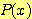 를 대입하면
를 대입하면 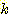 classes 의 경우의 Bayes' 정리는 다음과 같다.
classes 의 경우의 Bayes' 정리는 다음과 같다.
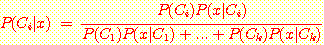 (B)
(B)
Example 3.1 에서, 만일 우리가 전체 모집단에서 열이 있을 확률  를 모르고, 감기인 사람이 열이 있을 확률
를 모르고, 감기인 사람이 열이 있을 확률 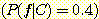 과 감기가 아닌 사람이 열이 있을 확률
과 감기가 아닌 사람이 열이 있을 확률 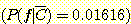 을 안다면, 사전 확률을 사용하여
을 안다면, 사전 확률을 사용하여  를 다음과 같이 구할 수 있다. (식 (A) 사용)
를 다음과 같이 구할 수 있다. (식 (A) 사용)
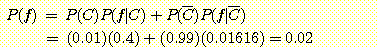
확률  는 사전확률 (prior probability) 라고 불리우는데 feature값을 알기 전에
모집단에서의 class 확률이기 때문이다. 사전 확률은 training set 이나 다른 상황에서
구해진다. 조건부 확률
는 사전확률 (prior probability) 라고 불리우는데 feature값을 알기 전에
모집단에서의 class 확률이기 때문이다. 사전 확률은 training set 이나 다른 상황에서
구해진다. 조건부 확률  는 사후확률 (posterior probability) 이라 불리우는데 feature 값을 발견한
후에 확률이기 때문이다.
는 사후확률 (posterior probability) 이라 불리우는데 feature 값을 발견한
후에 확률이기 때문이다.
Bayes' 정리 (B) 식을 이용하여 두 class (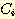 ,
, 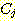 )사이의 likelihood ratio
)사이의 likelihood ratio 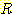 을 구할 수 있다.
을 구할 수 있다.
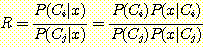
(B) 식에서의 오른쪽 식이 단순화 되어 계산이 쉬워지며 두 개의 class를 쉽게 비교한다.
단지 두 개의 class 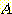 와
와 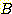 의 likelihood ratio 는 다음과 같다.
의 likelihood ratio 는 다음과 같다.

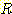 이 1 보다 크면 class
이 1 보다 크면 class 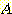 를 sample이 속하는 class 로 선택하고 1 보다 작으면
를 sample이 속하는 class 로 선택하고 1 보다 작으면 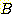 를 선택한다. class 멤버의 조건부 확률의 합은 1 이어야 하기 때문에 두 개의
class 만 있는 경우에
를 선택한다. class 멤버의 조건부 확률의 합은 1 이어야 하기 때문에 두 개의
class 만 있는 경우에 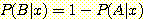 이므로 위의 식에 대입하면 다음이 얻어진다.
이므로 위의 식에 대입하면 다음이 얻어진다.

Example 3.2 ELISA test를 이용한 HIV virus 의 검출
어떤 환자가 HIV virus 가 걸린 것으로 의심되면
혈액의 항체를 검사하는 ELISA (enzyme linked immunosorbent assay) test를 하게된다.
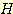 를 HIV virus를 가진 사건으로,
를 HIV virus를 가진 사건으로,  를 가지지 않은 사건으로, Pos 를 test에서 양성으로 나온 사건, Neg 는 음성으로
나온 사건으로 둔다. test에서 양성으로 나온 경우 환자가 HIV virus를 가질 확률
즉
를 가지지 않은 사건으로, Pos 를 test에서 양성으로 나온 사건, Neg 는 음성으로
나온 사건으로 둔다. test에서 양성으로 나온 경우 환자가 HIV virus를 가질 확률
즉 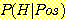 을 구하여 보자. 이 경우 임상에서 다음과 같은 확률을 가정한다.
을 구하여 보자. 이 경우 임상에서 다음과 같은 확률을 가정한다.

Bayes' 정리를 사용하여 다음과 같은 답을 구할 수 있다.
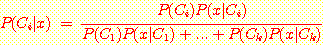
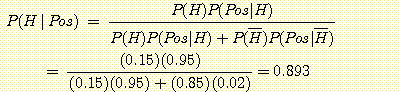
구해진 확률값이 0.5 보다 크기 때문에 해당 환자는 HIV virus일 확률이 높다고 결론짓는다.
다음과 같은 likelihood ratio를 사용해서도 같은 결과를 얻을 수 있다.
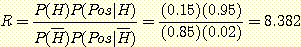
ratio 값이 1 보다 크기 때문에 HIV virus일 확률이
높다고 결론짓는다. 여기서 얻어진 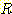 로부터 다음과 같이
로부터 다음과 같이 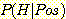 을 계산하여 Bayes' 정리로 얻어진 것과 같은 결과를 얻는다.
을 계산하여 Bayes' 정리로 얻어진 것과 같은 결과를 얻는다.
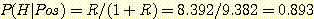
만일  나
나 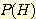 가 너무 작아서
가 너무 작아서  일 경우는 비록 test 가 양성이라도 virus 가 없는 것으로 결론이 날 것이다.
또한 병 자체보다도 test 에서의 error 가 있을 가능성도 있다. 많은 병원에서
일 경우는 비록 test 가 양성이라도 virus 가 없는 것으로 결론이 날 것이다.
또한 병 자체보다도 test 에서의 error 가 있을 가능성도 있다. 많은 병원에서 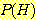 는 매우 낮기 때문에 첫 번째 test에서 양성이 나온 경우 두 번째 ELISA test를
하는 것을 기본으로 한다. 두 번째 test 가 양성일 경우 Western Blot test 를 하여
확인 test를 하게 된다. 비록 Western Blot test 가 ELISA test 보다 더 정확하지만
너무 비싸기 때문에 환자가 virus 에 걸렸다는 거의 확실한 증거가 없으면 시행하지
않는다.
는 매우 낮기 때문에 첫 번째 test에서 양성이 나온 경우 두 번째 ELISA test를
하는 것을 기본으로 한다. 두 번째 test 가 양성일 경우 Western Blot test 를 하여
확인 test를 하게 된다. 비록 Western Blot test 가 ELISA test 보다 더 정확하지만
너무 비싸기 때문에 환자가 virus 에 걸렸다는 거의 확실한 증거가 없으면 시행하지
않는다.
Bayes' 정리는 이산 분포(discrete distribution)
를 대신하여 continuous
densities 가 사용되더라도 거의 변화는 없다. 임의의 변수 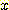 가 class
가 class 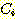 에 대해
에 대해 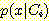 의 density를 가지고 사전확률이
의 density를 가지고 사전확률이  라고 가정하자. 임의의 변수가
라고 가정하자. 임의의 변수가 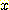 와
와 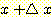 사이에 있는 사건을
사이에 있는 사건을 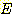 라 한다. class
라 한다. class 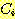 의 경우 이사건의 확률
의 경우 이사건의 확률 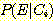 는 conditional density function 를 적분한 것이다.
는 conditional density function 를 적분한 것이다.
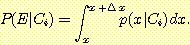
classes 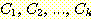 의 사건
의 사건 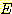 의 확률
의 확률
위의 그림에서 보라색 부분이
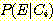 이다.
이다. 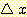 가 0 에 가까이 갈수록
가 0 에 가까이 갈수록 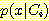 는 그 구간에서 상수값으로 근사하게 되고 보라색 부분은
는 그 구간에서 상수값으로 근사하게 되고 보라색 부분은 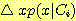 에 접근한다. 이것을 Bayes' 정리에 대입하면
에 접근한다. 이것을 Bayes' 정리에 대입하면
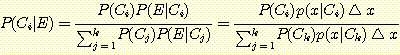
위 식의 분자와 분모를 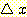 로 나누고 limit 를 취하면
로 나누고 limit 를 취하면
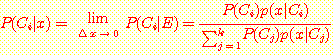
위 식은
continuous desities 의 경우의 Bayes' 정리이다. distribution functions 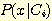 이 density functions
이 density functions 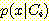 으로 바뀐 것 말고는 discrete 의 경우와 같다. 또한 likelihood ratio 도 같다.
으로 바뀐 것 말고는 discrete 의 경우와 같다. 또한 likelihood ratio 도 같다.

Example 3.3 ACT 점수에 따른 대학 응시자의 분류
Eastsoutheastern 주립대의 기록에 따르면, 신입생이
5 년 이내에 졸업할 확률은 0.8 이다. 5 년내에 졸업하는 학생의 ACT (American College
Test) 점수는 평균값 26 표준편차 2를 가지며 정규 분포한다. 5 년내에 졸업 못하는
학생의 점수는 평균값 22 표준편차 3를 가지며 정규 분포한다. 두가지 경우는 mutually
exclusive 사건이며 각각 두 개의 class 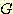 와
와 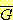 로 표현된다. 만일 한 학생의 ACT 점수가 22 라면 그 학생이 5 년내에 졸업할
확률을 구해보자.
로 표현된다. 만일 한 학생의 ACT 점수가 22 라면 그 학생이 5 년내에 졸업할
확률을 구해보자.
졸업할 사건 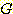 , 졸업 못하는 사건
, 졸업 못하는 사건 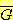 , 이때
, 이때 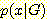 는
는  와
와  ,
, 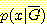 는
는  와
와  이고, 사전 확률
이고, 사전 확률  이며
이며 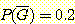 이다. 이때
이다. 이때
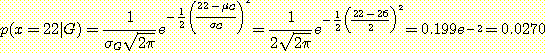
이며
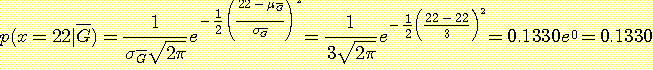
continuous density 의 경우의 Bayes' 정리에 대입하면
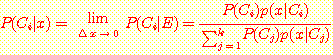
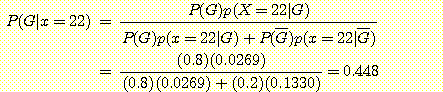
따라서 해당 학생은 졸업할 확률이 다소 낮은 것을 알 수 있다.
위의 경우와 달리 단지 졸업할 것이냐 아니냐 만을 구분하는 문제라면 다음의 likelihood ratio를 사용한다.

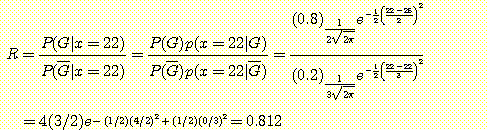
 이기 때문에 졸업 못할 확률이 높다는 것을 알 수 있다.
이기 때문에 졸업 못할 확률이 높다는 것을 알 수 있다.
 식에 대입하여 보면
식에 대입하여 보면
 가 구하여져 위의 값과 같다.
가 구하여져 위의 값과 같다.
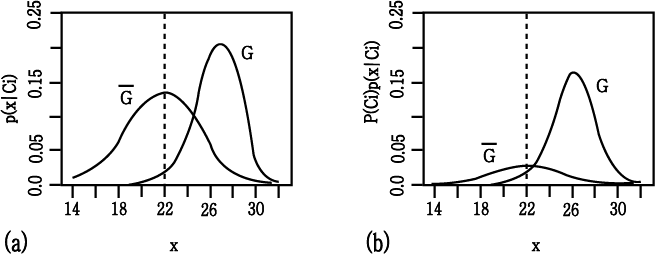
(a) ACT 점수의 조건부 density function (b) 사전 확률에 의해 가중치가 부여된 조건부 density function
continuous density 의 경우 class 의 사후확률
 를 비교하여 sample 들을 분류하는 다른 방법은 가장 가능성 있는 class에서
를 비교하여 sample 들을 분류하는 다른 방법은 가장 가능성 있는 class에서
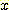 의 decision region을 계산하는 것이다. 각 decision region 은 하나의 class와
연관된다. feature value
의 decision region을 계산하는 것이다. 각 decision region 은 하나의 class와
연관된다. feature value 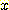 로서 sample을 분류하기 위해
로서 sample을 분류하기 위해 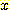 를 포함하는 decision region을 결정하고
를 포함하는 decision region을 결정하고 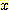 를 해당 지역의 class 에 할당한다. decision region 사이의 경계를 decision
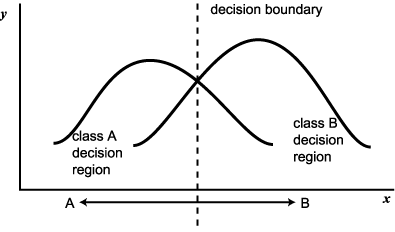
boundary 라고 한다. 적절한 decision boundary는 feature space를
를 해당 지역의 class 에 할당한다. decision region 사이의 경계를 decision
boundary 라고 한다. 적절한 decision boundary는 feature space를  으로 구분하여,
으로 구분하여, 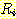 에서의
에서의 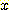 의 값이 어떤 다른 class 보다
의 값이 어떤 다른 class 보다 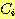 에 속할 확률이 높도록 한다. 만일 feature value 가 두 class 사이의 decision
boundary 상에 있다면 두 개의 class 에 속할 확률은 같다. 두 class
에 속할 확률이 높도록 한다. 만일 feature value 가 두 class 사이의 decision
boundary 상에 있다면 두 개의 class 에 속할 확률은 같다. 두 class 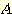 와
와 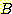 사이의 적절한 decision boundary를 계산하기 위해, 만일 density 가 continuous
하고 overlapping되었다면 그들의 사후확률이 같다고 할 수 있다.
사이의 적절한 decision boundary를 계산하기 위해, 만일 density 가 continuous
하고 overlapping되었다면 그들의 사후확률이 같다고 할 수 있다.

Bayes' 정리를 대입하고 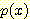 를 제거하면
를 제거하면

at the optimal decision boundary.
만일 각 class 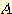 와
와 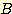 각각의 feature
각각의 feature
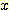 가 정규 분포한다면 다음과 같이 된다.
가 정규 분포한다면 다음과 같이 된다.
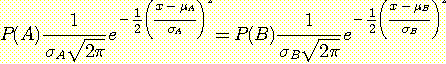
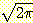 를 제거하고 양변에 natural log를 취하고 -2를 곱하면
를 제거하고 양변에 natural log를 취하고 -2를 곱하면
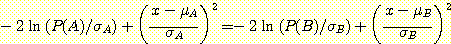
적절한 decision boundaries 는
이 방정식을 만족하는 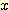 값에 위치한다. 위의 방정식은 다음과 같은 discriminant function 으로 변환
될 수 있다.
값에 위치한다. 위의 방정식은 다음과 같은 discriminant function 으로 변환
될 수 있다.
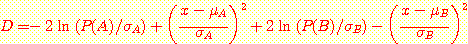
 가 0 인 지점이 decision boundary 이다.
가 0 인 지점이 decision boundary 이다.  가 양수이면 class
가 양수이면 class 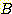 일 확률이 높고
일 확률이 높고  가 음수면 class
가 음수면 class 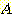 일 확률이 높다.
일 확률이 높다.
Example 3.4 적절한 1 차원 decision boundary 의 계산
Example 3.3 의 경우 decision boundaries 를 계산하기 위한 식에 아래 data 를 대입한다.
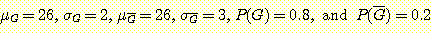
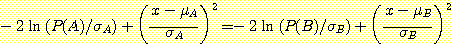
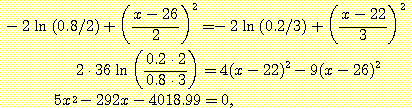
위의 과정을 통해 다음의 값이 구해진다.
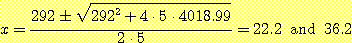
이러한 두 개의 decision boundary 는 feature space를 3 개의 decision region 으로 나누고 다음의 decision rule을 만든다.
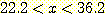 라면 sample을 class
라면 sample을 class 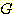 로 분류한다.
로 분류한다.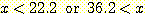 라면 sample 을 class
라면 sample 을 class 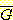 로 분류한다.
로 분류한다. 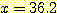 에서의 decision boundary 는 두 class 의 평균값에서 너무 멀리 떨어져 있어(약
five standard deviation 만큼) 3 백만중 하나 이하의 sample 만이 class
에서의 decision boundary 는 두 class 의 평균값에서 너무 멀리 떨어져 있어(약
five standard deviation 만큼) 3 백만중 하나 이하의 sample 만이 class 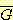 를 위한 위쪽 decision region 에 놓여있게 된다 (각 그룹의 ACT 점수가 정규분포한다는
가정하에). 실제의 경우에는 feature들은 정확하게 정규분포 하지는 않을 것이다.
명확히
를 위한 위쪽 decision region 에 놓여있게 된다 (각 그룹의 ACT 점수가 정규분포한다는
가정하에). 실제의 경우에는 feature들은 정확하게 정규분포 하지는 않을 것이다.
명확히  에 속하는 어떤 학생도 졸업가능하여
에 속하는 어떤 학생도 졸업가능하여  로 분류되어야 할 것이므로 이러한 경우에는 단지 하나의 decision boundary
만이 의미가 있을 것이다. 이러한 모델에서는 가능한 부정확성을 수정하기
위하여, 적절한 크기의 data set을 사용하고
로 분류되어야 할 것이므로 이러한 경우에는 단지 하나의 decision boundary
만이 의미가 있을 것이다. 이러한 모델에서는 가능한 부정확성을 수정하기
위하여, 적절한 크기의 data set을 사용하고 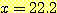 부근에서 다양한 decision boundary 에 의해 만들어진 분류의 정확성을 비교하여
설계를 정밀화해야 할 것이다.
부근에서 다양한 decision boundary 에 의해 만들어진 분류의 정확성을 비교하여
설계를 정밀화해야 할 것이다.
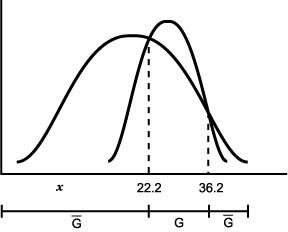
 , the
, the 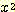
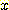
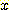
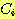

사전 확률과 조건부 확률에 의해
계산되어진 사후 확률의 그림 (  와
와 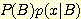 ) 이다. (a) 두 점에서 교차한다 (two real roots), (b) 한점에서 교차 하는
것으로 일반적인 그림이다 (one real root). (c) 접해있는(tangent) 그림으로 decision
boundary 가 없다(a repeated real root),
(d) 교차점이 없으며 전부 A class 라고 주장하는 것이 가능하다(no real root).
) 이다. (a) 두 점에서 교차한다 (two real roots), (b) 한점에서 교차 하는
것으로 일반적인 그림이다 (one real root). (c) 접해있는(tangent) 그림으로 decision
boundary 가 없다(a repeated real root),
(d) 교차점이 없으며 전부 A class 라고 주장하는 것이 가능하다(no real root).
....................
만일 class 들이 feature공간에서
넓게 떨어져 있지 않으면 single feature 로서 class 들을 잘 식별해 낼 수는 없다.
그러나 두 개 이상의 feature가 사용된다면 여러개의 class 들을 잘 식별해 낼 수
있을 것이다. 여러개의 feature (multiple feature) 를 가진 경우의 Bayes' 정리는
single feature 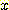 의 값을 feature vector x (구성 요소로서 single feature를 가짐)의 값으로
바꾸어 주면 된다.
의 값을 feature vector x (구성 요소로서 single feature를 가짐)의 값으로
바꾸어 주면 된다.
이산값(discrete)을
가지는 경우에 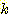 개의 class에 대해 다음의 Bayse' 정리가 얻어진다. 여기서
개의 class에 대해 다음의 Bayse' 정리가 얻어진다. 여기서 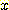 는 vector x 이다.
는 vector x 이다.
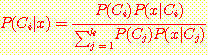
연속값 (continuous)을
가지는 경우의 Bayes' 정리는 조건 확률 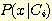 를 조건 밀도( conditional density)
를 조건 밀도( conditional density) 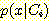 로 바꿔주면 된다.
로 바꿔주면 된다. 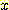 는 vector x 이다.
는 vector x 이다.
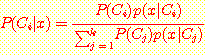
Example 3.7 ACT 점수와 class rank 를 사용한 대학 응시자의 분류
Example 3.3 에서 ACT 점수
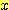 에 의해 대학 응시자를 분류하는 것에 더해서,응시자의 고등학교 에서의 성적
백분율에 따른 등수
에 의해 대학 응시자를 분류하는 것에 더해서,응시자의 고등학교 에서의 성적
백분율에 따른 등수 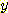 를 사용해서 분류한다고 가정하자.
를 사용해서 분류한다고 가정하자. 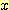 와
와 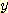 의 conditional density 가 bivariate normal 이라고 가정한다. (
의 conditional density 가 bivariate normal 이라고 가정한다. ( 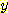 는 백분율이기 때문에 uniformly distribute 한다. 그러나 이것이 특정 대학의
응시자에게있어 normally distribute 하지 못하게 하는 것은 아니다.)
는 백분율이기 때문에 uniformly distribute 한다. 그러나 이것이 특정 대학의
응시자에게있어 normally distribute 하지 못하게 하는 것은 아니다.)
class 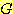 를 위한 인수는
를 위한 인수는  ,
,  ,
, 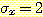 ,
,  ,
,  ,
,  이다.
이다.
class 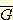 를 위한 인수는
를 위한 인수는 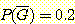 ,
,  ,
, 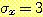 ,
,  ,
,  ,
,  이다.
이다.
위의 경우 ACT 점수 22 이며 학급등수가 70 등인 응시자가 5 년내에 졸업할 확률은 얼마인가?
bivariate normal density 식은 다음과 같이 표현된다.
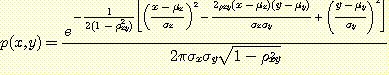
class 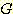 에 대한 위의 인수 값을 대입하면
에 대한 위의 인수 값을 대입하면
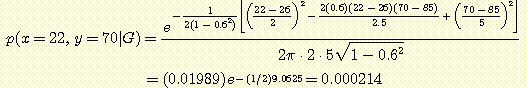
class 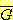 에 대한 위의 인수 값을 대입하면
에 대한 위의 인수 값을 대입하면
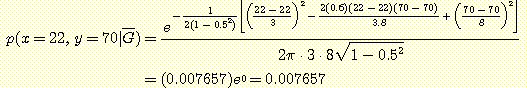
continuous density 의 경우의 Bayes' 정리
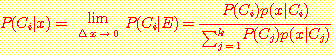
위의 식을 사용하여 사후확률을 다음과 같이 구한다.
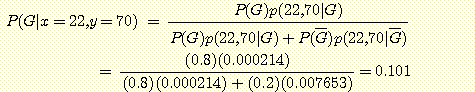
ACT 점수 22 이며 학급등수가 70 등인 응시자가 5 년내에 졸업할 확률은 10 % 임을 알 수 있다.
2개 이상의 feature 가 사용될 때
multivariate normal density 의 지수는 각 feature 들의 쌍의 곱, feature 의
제곱과 linear term 등을 포함하는 일반적인 2 차식이다. 만일 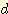 features 의 경우라면
features 의 경우라면  terms을 결과한다.
terms을 결과한다. 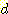 가 중간정도의 값을 가질 경우 만일 matrix notation 이 사용되지 않는다면
표현하기가 어렵게 된다.
가 중간정도의 값을 가질 경우 만일 matrix notation 이 사용되지 않는다면
표현하기가 어렵게 된다. 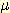 는 mean vector 이고
는 mean vector 이고 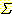 는 covariance matrix 이다. 이 경우 multivariate normal density 는 다음과
같다.
는 covariance matrix 이다. 이 경우 multivariate normal density 는 다음과
같다.
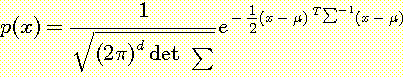
.....................
하나의 문제에서 여러개의 이산 feature가
있을 경우, 각 class를 위한 feature값들의 모든 가능한 조합의 확률을 추정해 낼
정도로 충분한 sample이 있을 수는 없다. 즉 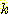 개의 class를 가지고
개의 class를 가지고 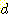 개의 feature와 각 feature가
개의 feature와 각 feature가 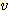 개의 값을 가진다고 하자. 이때는
개의 값을 가진다고 하자. 이때는 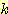 개의 class 각각에 대해
개의 class 각각에 대해 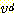 개의 가능한 사건이 있을 수 있고, 따라서
개의 가능한 사건이 있을 수 있고, 따라서  개의 가능한 데이터 조합이 가능하다.
개의 가능한 데이터 조합이 가능하다.
예를 들면 질병 진단에 있어서 10
가지의 증상이 있고 각각의 증상에 대해 4 개의 가능한 답변이 있을 수 있다고 했을
때 3 개의 병중에서 어떤 병인지를 식별해 내는 간단한 경우가 있다고 하자. 이때
가능한 경우의 수는 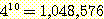 개 이고
개 이고 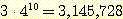 개의 사건의 조합이 가능하다. 그 각각에 대해 확률값이 구해져야 한다. 만일
이전에는 발병한 적이 없는 새로운 종류의 질병의 경우라면 어떤 추가적인 가정을
하지 않고는 3 개의 질병의 확률을 추정할 방법은 없을 것이다.
개의 사건의 조합이 가능하다. 그 각각에 대해 확률값이 구해져야 한다. 만일
이전에는 발병한 적이 없는 새로운 종류의 질병의 경우라면 어떤 추가적인 가정을
하지 않고는 3 개의 질병의 확률을 추정할 방법은 없을 것이다.
가능한 조합의 수를 감소시키는 하나의
방법은 각 class 에 주어진 feature 가 독립적이라고 가정하는 것이다. 그러면 다양한
feature vector 의 확률이 곱하기를 하여 추정될 수 있다. 즉 질병 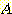 의 경우에 feature vector 가 값
의 경우에 feature vector 가 값  을 가질 확률은 다음과 같이 구해진다.
을 가질 확률은 다음과 같이 구해진다.
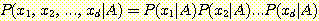
위와 같이 하면
 이 아니라
이 아니라  개 만큼의 확률값만 구해보면 된다
개 만큼의 확률값만 구해보면 된다
전체 모집단에 대해 feature 들이
독립적이라고 가정하여  를
를 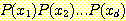 로 바꾸는 것은 잘못일 것이다. 왜냐하면 이러한 가정이 이용할 수 있는 data
와 모순되어 class 멤버의 모든 사후확률의 합이 1 이 아닐 것이기 때문이다.
로 바꾸는 것은 잘못일 것이다. 왜냐하면 이러한 가정이 이용할 수 있는 data
와 모순되어 class 멤버의 모든 사후확률의 합이 1 이 아닐 것이기 때문이다.
이러한 두 가정을 이해하기 위하여,
다음 그림의 (a) 는 연속 feature 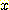 와
와 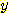 상의 두 class 가 사각형위에 uniformly distribute 하는 것을 보여준다. feature
상의 두 class 가 사각형위에 uniformly distribute 하는 것을 보여준다. feature
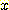 와
와 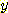 는 각 class 내에서 독립적이다. 예를들면 만일 class 가
는 각 class 내에서 독립적이다. 예를들면 만일 class 가 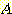 라는 것을 알면
라는 것을 알면 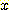 를 알아도
를 알아도 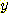 에 대한 어떤 부가적인 정보도 주지 않는다. 그래서
에 대한 어떤 부가적인 정보도 주지 않는다. 그래서 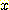 와
와 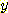 는 class
는 class 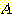 의 멤버에 대하여 독립적이다. 또한 class
의 멤버에 대하여 독립적이다. 또한 class 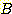 에 대해서도 마찬가지다. 그러나 feature
에 대해서도 마찬가지다. 그러나 feature 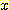 와
와 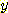 는 전체 모집단에 대해서는 독립적이지 않다. 실제로 만일
는 전체 모집단에 대해서는 독립적이지 않다. 실제로 만일 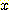 가 가능한 범위의 높은 부분에 있다면
가 가능한 범위의 높은 부분에 있다면 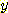 도 또한 그 범위의 높은 부분에 있어야 한다. 그래서
도 또한 그 범위의 높은 부분에 있어야 한다. 그래서 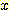 와
와 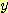 는 그 모집단에서 positively correlated 되어있다.
는 그 모집단에서 positively correlated 되어있다.
반면에 다음 그림 (b) 는 삼각형
내에서 uniformly distribute 하는 class 들을 보여준다. 이 경우
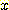 와
와 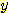 는 전체 모집단에서는 독립적이지만 각 class 에서는 그렇지 않다. 만일 class를
모르는 경우
는 전체 모집단에서는 독립적이지만 각 class 에서는 그렇지 않다. 만일 class를
모르는 경우 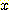 를 알아도
를 알아도 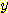 에 대해서는 어떤 정보도 알 수 없다. 그러나 만일 class 가
에 대해서는 어떤 정보도 알 수 없다. 그러나 만일 class 가 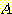 라는 것을 알고
라는 것을 알고 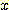 가 크다는 것을 알면
가 크다는 것을 알면 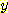 가 가능한 범위의 아래쪽에 있다는 것을 의미한다.
가 가능한 범위의 아래쪽에 있다는 것을 의미한다.
density 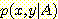 와
와 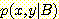 는 각 사각형 또는 삼각형내에서 일정하며
는 각 사각형 또는 삼각형내에서 일정하며 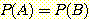 이라고 가정한다.
이라고 가정한다.
(a) Feature 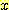 와
와 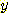 는 각 class 내에서 독립적이지만 전체 모집단에서는 그렇지 않다.
는 각 class 내에서 독립적이지만 전체 모집단에서는 그렇지 않다.
(b)
Feature 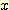 와
와 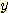 는 전체 모집단에서는 독립적이지만 각 class 들은 그렇지 않다.
는 전체 모집단에서는 독립적이지만 각 class 들은 그렇지 않다.
만일 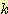 classes 와
classes 와 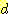 features 가 있다면, feature 들이 각 class 내에서 독립적이라고 가정할 때
features 가 있다면, feature 들이 각 class 내에서 독립적이라고 가정할 때
 를 계산하기 위해 feature 들이 모집단 내에서 독립적이라고 가정할 필요는
없다. 다음의 식은
를 계산하기 위해 feature 들이 모집단 내에서 독립적이라고 가정할 필요는
없다. 다음의 식은
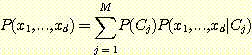
각 class 내에서 다음의 가정 하에서만 계산될 수 있다.
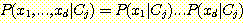
위의 두식을 multiple feature 의 경우의 다음 Bayes' 정리에 대입하면
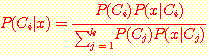
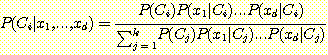
class 가 독립적이라고 가정함으로써 이전에는 결코 볼 수 없었던 feature 들의 조합들을 위한 class 멤버의 확률을 추정할 수 있다. 그러나 만일 독립적이라는 가정이 사실이 아니라면 이러한 확률 추정치 각각은 error를 발생시킬 것이다. 만일 data 가 이용가능하다면, chi-squared test 같은 통계적 test를 사용하여 feature 들이 독립적이라는 가설을 test 할 수 있다.
class 에 주어진 feature들이 독립적이라고
가정함으로써,  로 부터
로 부터 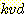 까지 축적되어야만 하는 data 의 가능한 조합의 수를 감소시킨다 (
까지 축적되어야만 하는 data 의 가능한 조합의 수를 감소시킨다 (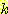 classes 와
classes 와 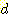 features, 각 feature 에 대한
features, 각 feature 에 대한 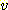 values를 가정할 때), 위에서
values를 가정할 때), 위에서 
 의 경우에 축적된 data 의 양이 3,145,728 개의 조합이 필요하였다. 그러나
만일 feature 들이 독립적이라고 가정한다면, 단지
의 경우에 축적된 data 의 양이 3,145,728 개의 조합이 필요하였다. 그러나
만일 feature 들이 독립적이라고 가정한다면, 단지 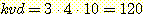 개의 조합만 고려하면 된다. 이러한 방법의 단점은, 만일 feature 들이 실제로
conditionally independent
하지 않다면 그 결과가 bias 될 수 있다는 것이다.
개의 조합만 고려하면 된다. 이러한 방법의 단점은, 만일 feature 들이 실제로
conditionally independent
하지 않다면 그 결과가 bias 될 수 있다는 것이다.
Example 3.10 두 번의 ELISA test를 사용한 HIV virus 의 검출
Example 3.2 에서 논의한 단 한번의 ELISA test 만으로는 충분히 정확한 결과를 보이지 않는데, 특히 주어진 모집단에서 HIV virus 의 사전확률이 낮을 때 그렇다. 따라서 첫 번째 test 가 양성일 때 두 번째 ELISA test 가 보통 행해진다.
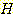 를 HIV virus를 가진 사건으로,
를 HIV virus를 가진 사건으로,  를 가지지 않은 사건으로, Pos 를 첫 번째 test에서 양성으로 나온 사건, Neg 는 음성으로
나온 사건으로 둔다. 두 번의 독립적인 test 가 행해질 때
를 가지지 않은 사건으로, Pos 를 첫 번째 test에서 양성으로 나온 사건, Neg 는 음성으로
나온 사건으로 둔다. 두 번의 독립적인 test 가 행해질 때  는 첫 번째는
는 첫 번째는 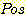 두 번째는
두 번째는  의 경우이고,
의 경우이고, 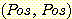 는 두 번의 test 가 모두 양성인 경우이다. 이 경우 임상에서 다음과 같은 확률을 가정한다.
는 두 번의 test 가 모두 양성인 경우이다. 이 경우 임상에서 다음과 같은 확률을 가정한다.

각 class 내에서 test 들이 독립적이라고 가정하면 곱셈법칙에 의해 다음이 구해진다.
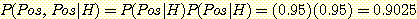

Bayes' 정리에 의하여
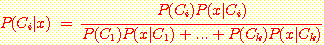
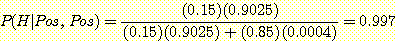
즉 두 번의 ELIZA test 가 주어지고 둘다 양성이라면 그 환자가 HIV virus 일 확률은 매우 높은 확률 (0.997)을 보인다. 반면에 단지 한번의 ELIZA test 만으로는 Example 3.2 에서 본대로 훨씬 적은 확률 (0.893)을 보인다.
실제로는 두 번의 test 사이에 독립적이라는 가정이 정당한지를 결정하기 위해 부가적인 data 가 요구될 것이다. 만일 test 결과가 부정확하게 나온 경우 그것이 실험실 과정에서의 임의의 변화무쌍함 때문이라면 그 결과는 독립적일 수 있다. 그러나 그것이 환자의 혈액에서 어떤 일정한 비정상 때문이라면 그 결과는 독립적일 수 없다.
..................
연속값을 가지는 두변수 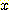 ,
, 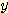 가 있을 때 두 개의 class 인
가 있을 때 두 개의 class 인 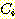 와
와 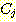 는 서로 중첩되는 범위를 가지며 그 사이에 적절한 decision boundary (2차원)
가 존재한다.
는 서로 중첩되는 범위를 가지며 그 사이에 적절한 decision boundary (2차원)
가 존재한다.
그것을  라고 할 수 있고 그로부터 Bayes' 정리를 사용하여 다음 식이 얻어진다.
라고 할 수 있고 그로부터 Bayes' 정리를 사용하여 다음 식이 얻어진다.
 ---- (1)
---- (1)
각 class 가 이항 정규 분포를 가진다고 가정하면 다음 식이 (1) 의 양변에 이용된다.
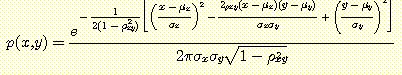 ---- (2)
---- (2)
2 개의 이항 분포 class를 위해 적절한 decision boundary 방정식(위의 (1)식) 은 양변에 log를 취하여 직선이나 원뿔형의 (타원, 포물선, 쌍곡선) 식으로 축소된다.
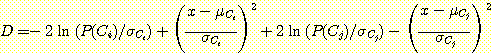
위의 식을 decision function or discriminant function 이라고 한다.
Example 3.12 적절한 decision boundary 의 결정 (feature 들이 각 class 내에서 독립적일 때 두 개의 단순한 bivariate normal class 들 사이)
class 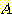 와
와 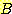 가 둘다 bivariate normal 이며 사전확률
가 둘다 bivariate normal 이며 사전확률 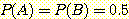 를 가지고 있다고 가정한다. class
를 가지고 있다고 가정한다. class 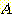 의 conditional density를 위한 인수는
의 conditional density를 위한 인수는  이며 class
이며 class 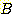 의 인수는
의 인수는  이다.
이다.
각 class들을 위한  이기 때문에 bivariate normal density 는 simple form을 가진다. 실제로
이기 때문에 bivariate normal density 는 simple form을 가진다. 실제로
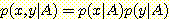 이며
이며 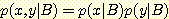 이다. 다음 식에 대입하면
이다. 다음 식에 대입하면

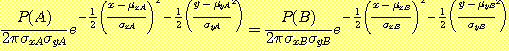
두 개의 weighted densities를 같게놓고 인수를 대입하면
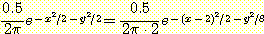
 를 제거하고 양변에 natural log 를 취하면
를 제거하고 양변에 natural log 를 취하면
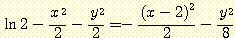
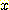 가 class
가 class 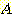 와 class
와 class 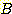 가 같은 variance를 가지기 때문에
가 같은 variance를 가지기 때문에 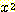 terms 는 제거되고 포물선모양의 decision boundary를 보인다.
terms 는 제거되고 포물선모양의 decision boundary를 보인다.
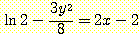 또는
또는 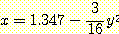
점선의 포물선이 본 예제를 위한
decision boundary 이다. 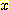 -axis
-axis
어떠한 normal density function
 (
( 는 양의 상수) 을 위한 일반적인 확률 밀도의 모양은 항상 타원형이다. 왜냐하면
만일
는 양의 상수) 을 위한 일반적인 확률 밀도의 모양은 항상 타원형이다. 왜냐하면
만일 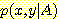 이 상수라면, density function에서 2 차 지수 (quadratic exponent) 는 항상
상수이어야 하기 때문이다.
이 상수라면, density function에서 2 차 지수 (quadratic exponent) 는 항상
상수이어야 하기 때문이다.
따라서 class 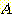 즉
즉 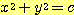 의 경우 그 모양이 (0,0) 이 중심인 원모양이다(원은 타원의 특별한 경우이다). class
의 경우 그 모양이 (0,0) 이 중심인 원모양이다(원은 타원의 특별한 경우이다). class 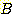 즉
즉  의 경우는 (2,0) 이 중심인 타원형이다. 그것은 기울어지지 않았으며 (class
의 경우는 (2,0) 이 중심인 타원형이다. 그것은 기울어지지 않았으며 (class 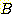 의 경우는
의 경우는  이기때문) 따라서
이기때문) 따라서 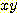 -term 이 없다. 그것의 major axis 는
-term 이 없다. 그것의 major axis 는 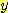 -axis 에 평행하며, 어떤
-axis 에 평행하며, 어떤  값에 대해서도 minor axis 길이의 2배이다. 일반적인 확률밀도의 모양의 일부를
위의 그림에서 볼 수 있다. 타원형의 중심에서
값에 대해서도 minor axis 길이의 2배이다. 일반적인 확률밀도의 모양의 일부를
위의 그림에서 볼 수 있다. 타원형의 중심에서 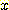 와
와 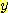 방향으로
방향으로 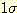 와
와 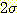 만큼 떨어진 위치에 두 개의 타원이 있다.
만큼 떨어진 위치에 두 개의 타원이 있다.
예를들면  의 경우 하나의
의 경우 하나의 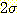 모양의 점은
모양의 점은 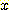 -축에서
-축에서  로부터 four units 에 있을 것이다.
로부터 four units 에 있을 것이다. 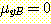 의 경우에 이 점은
의 경우에 이 점은 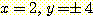 에 있다.
에 있다.
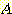 와
와 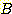 decision region을 구분하는 decision boundary 는 다음과 같다.
decision region을 구분하는 decision boundary 는 다음과 같다.
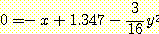
다음의 discriminant function 이 구해진다.
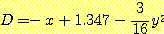
만일 위의 그림에서  이고
이고 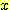 가 크다면 그 점은 decision region
가 크다면 그 점은 decision region 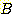 에 존재하고
에 존재하고  는 음수일 것이다.
는 음수일 것이다.  는 class
는 class 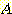 decision region 에서는 양수이다.
decision region 에서는 양수이다.
feature vector 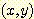 를 가지는 하나의 sample 은
를 가지는 하나의 sample 은  를 계산하고 그 부호를 앎으로써 분류될 수 있다. 이때 그 sample을 분류하기
위해
를 계산하고 그 부호를 앎으로써 분류될 수 있다. 이때 그 sample을 분류하기
위해 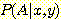 나
나 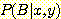 을 계산할 필요는 없다.
을 계산할 필요는 없다.
..............
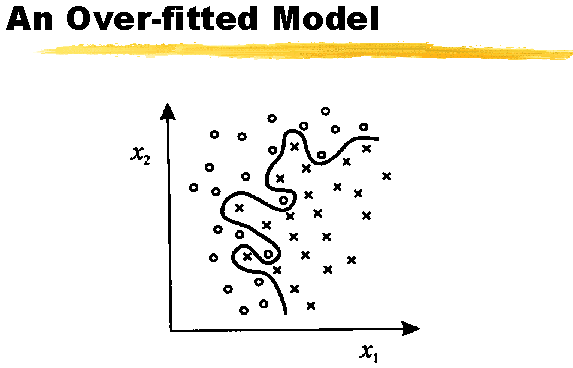
................
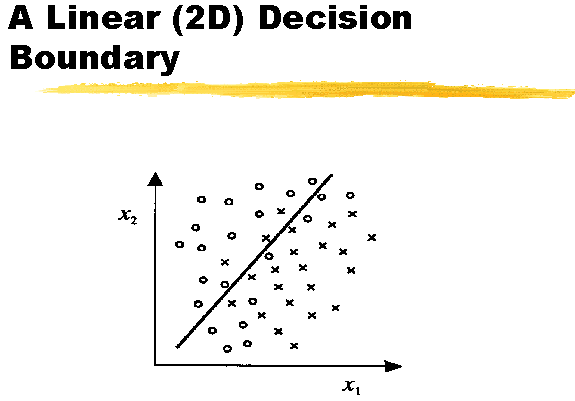
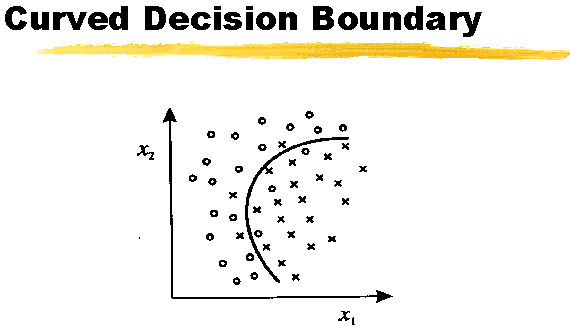
decision boundary 는 다음과 같은 종류가 있다.
(a) 선형
decision boundary  (b)
원형(circular) decision boundary
(b)
원형(circular) decision boundary  . sample 이 밀접하면 원형으로 나타난다.
. sample 이 밀접하면 원형으로 나타난다.
(a) 포물선(parabolic)
decision boundary  (b)
타원형(elliptical) decision boundary
(b)
타원형(elliptical) decision boundary  .
.
(a) 쌍곡선(hyperbolic)
decision boundary. 2 개의 decision boundary 가 존재  (b)
교차되는 선형 decision boundary
(b)
교차되는 선형 decision boundary  이것은 쌍곡선 decision boundary 의 변형이다.
이것은 쌍곡선 decision boundary 의 변형이다.
....................